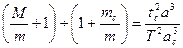
Как определяют массу планет
Массы небесных тел можно измерить разными способами:
- Путем измерения силы тяжести на поверхности данного небесного тела (гравиметрический способ).
- По третьему обобщенному закону Кеплера.
Первый способ применительно к Земле рассматривается тут.
Прежде чем рассматривать второй способ, проверим выполнение третьего закона Кеплера для случая кругового движения планеты со скоростью (v_{к}).
Пусть тело массой (m) движется с линейной скоростью (v_{к}) вокруг тела (M) ((m ≪ M)) по окружности радиуса (r_{к}). Это возможно, если движение происходит под действием силы, создающей центростремительное ускорение (a = frac{v_{к}^{2}}{r_{к}}). Силой, создающей ускорение, является сила тяготения, равная (frac{GMm}{r_{к}^{2}}). Приравнивая (frac{v_{к}^{2}}{r_{к}}) к ускорению (frac{GM}{r_{к}^{2}}), создаваемому тяготением, получим, что [v_{к}^{2} = frac{GM}{r_{к}}.]
Если период обращения тела (m) вокруг тела (M) составляет время (T), то линейная скорость движения этого тела по орбите равна [v_{к} = frac{2πr_{к}}{T}.]
Подставляя (v_{к} = frac{2πr_{к}}{T}) в (v_{к}^{2} = frac{GM}{r_{к}}), получим: (left (2πfrac{r_{к}}{T} right )^{2} = frac{GM}{r_{к}}), или [frac{r_{к}^{2}}{T^{2}} = frac{GM}{4π^{2}}.]
Для эллиптического движения формула (frac{r_{к}^{2}}{T^{2}} = frac{GM}{4π^{2}}) также справедлива, если вместо радиуса окружности (r_{к}) подставить большую полуось (a) эллиптической орбиты. В таком случае получим соотношение: [frac{a^{3}}{T^{2}M} = frac{G}{4π^{2}},] которое можно сформулировать следующим образом: отношение куба большой полуоси орбиты тела к квадрату периода его обращения и массе центрального тела есть величина постоянная.
Если массой (m) меньшего тела нельзя пренебрегать по сравнению с массой (M) центрального тела, то в третий закон Кеплера, как показал Ньютон, вместо массы (M) войдет сумма масс ((M + m)) и соотношение (frac{a^{3}}{T^{2}M} = frac{G}{4π^{2}}) запишется в виде: [frac{a^{3}}{T^{2}(M + m)} = frac{G}{4π^{2}}.]
Обобщив формулу (frac{a^{3}}{T^{2}(M + m)} = frac{G}{4π^{2}}) для двух небесных тел массами (M_{1}) и (M_{2}), получим: [frac{T_{1}^{2}(M_{1} + m_{1})}{T_{2}^{2}(M_{2} + m_{2})} = frac{a_{1}^{3}}{a_{2}^{3}},] т. е. квадраты сидерических периодов спутников ((T_{1}^{2}) и (T_{2}^{2})), умноженные на сумму масс главного тела и спутника ((M_{1} + m_{1}) и (M_{2} + m_{2})), относятся как кубы больших полуосей орбит спутников ((a_{1}^{3}) и (a_{2}^{3})).
На основе уточненного Ньютоном третьего закона Кеплера можно вычислить массы планет имеющих спутники, вторым способом, а также вычислить массу Солнца.
Массы планет, не имеющих спутников, могут быть определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, а также по возмущениям, производимым ими друг на друга.
Источник: ed-lib.ru
Ответ 2. Массу планеты, имеющей спутник, очень легко рассчитать по характеристикам движения спутника. Хотя орбиты движения спутников эллиптические, но степень эллиптичности обычно очень мала и с хорошей точностью орбиту можно считать круговой. Для устойчивого движения всегда выполняется равенство гравитационной силы притяжения и центробежной силы: γmM/R² = mV²/R, где m — масса спутника, M — масса планеты, V — скорость движения спутника, R — расстояние от спутника до планеты. Сокращаем массу спутника m и получаем M = RV²/γ. Расстояние R легко измеряется с помощью телескопов: смотрят на спутник и саму планету из двух точек земной поверхности и видят их под разными углами, затем простейшими формулами геометрии высчитывают расстояние до спутника и планеты, а разность между этими расстояниями и дает искомую величину R. Зная удаление спутника от планеты и время его полного обращения, легко находят скорость V. И окончательно узнают массу планеты М. А затем вводят поправки на эллиптичность орбиты и корректируют найденную массу. Определить массу планеты, не имеющей спутников (Венера и Меркурий) , заметно сложнее.
ычно это делается через гравитационные возмущения орбит. Чем ближе подходит Венера к Земле, тем сильнее притягивает её Земля и Венера как-бы немножко сходит со своей орбиты (Земля при этом также сходит) . Это изменение орбиты и называется гравитационным возмущением. Оно настолько мало, что даже в долгосрочной перспективе никак не скажется на судьбе планет. Но уже достаточно велико, чтобы быть обнаруженным в телескопы. Величина гравитационных возмущений орбит пропорциональна массам планет. Зная массу Земли, всегда можно подобрать такое значение массы Венеры, чтобы рассчитаннное возмущение орбиты совпало с тем, что наблюдается на практике. А затем точно таким же макаром ищут массу Меркурия. Массу звезд ищут иным способом. Вначале находят массу Солнца по той же самой формуле, что я написал выше. Затем выбирают некоторую звезду и снимают максимально возможную информацию её излучения: светимость, спектр, распределение энергии по спектру, наличие линий поглощения и излучения в спектре, величину красного смещения и т. д. И все это сравнивают с теми же данными по Солнцу. Дело в том, что некоторые характеристики излучения звезды зависят от её массы. Сравнивая эти данные с данными Солнца и зная массу последнего, можно определить массу звезды. ( отв. Гений) #наука
Источник: ok.ru
Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела — его массу.
Массу можно определить:
а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),
б) по третьему уточнённому закону Кеплера,
в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.
1. Первый способ применяется на Земле.
На основании закона тяготения ускорение g на поверхности Земли:

где m — масса Земли, а R — её радиус.
m = (gR2)/G.
g и R измеряются на поверхности Земли. G = const.
С принятыми сейчас значениями g, R, G получается масса Земли:
m = 5,976 .1027г = 6 .1024кг.
Зная массу и объём, можно найти среднюю плотность. Она равна 5,5 г/см3.
2. По третьему закону Кеплера можно определить соотношение между массой планеты и массой Солнца, если у планеты есть хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг неё.

где M, m, mc- массы Солнца, планеты и её спутника, T и tc- периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а и ас— расстояния планеты от Солнца и спутника от планеты соответственно.
Из уравнения следует

Отношение М/m для всех планет очень велико; отношение же m/mc, очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь.
Соотношение М/m можно легко найти из уравнения.
Для случая Земли и Луны нужно сначала определить массу Луны. Это сделать очень сложно. Решается задача путём анализа возмущений в движении Земли, которые вызывает Луна.
3. По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые "лунным неравенством". Наличие этого факта в видимом движении Солнца указывает на то, что центр Земли описывает небольшой эллипс в течение месяца вокруг общего центра масс "Земля — Луна", расположенного внутри Земли, на расстоянии 4650 км. от центра Земли.
Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 — 1931 гг.
По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81,30.
В 1964 году Международный астрономический союз принял его как const.
Из уравнения Кеплера получаем для Солнца массу = 2.1033г., что в 333000 раза превосходит земную.
Массы планет, не имеющих спутников, определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, по возмущениям, производимым ими друг на друга.
Источник: studopedia.org