Формы и размеры земли геодезия
Предмет и задачи инженерной геодезии
Геодезия — наука, изучающая форму и размеры Земли, геодезические приборы, способы измерений и изображений земной поверхности на планах, картах, профилях и цифровых моделях местности. В процессе развитии геодез. в ней выделились ряд связанных между собой научных дисциплин. Назовём те которые нужн учитывать или исп. в геодезич. обеспечении строительства:
— высшая геодезия ( изучает методы определения формы и размеров Земли)
— топография и гидрография развивают методы съемки участков земной поверхности и изображения их на плоскости в виде карт, планов и профилей;
— фотограмметрия занимается обработкой фото-, аэрофото- и космических снимков для составления карт и планов;
— картография- изучает теоретические основы картографических проекций и технологию созд. карт различн. масштабов;
— маркшейдерия — область геодезии, обслуживающая горнодобывающую промышленность и строительство тоннелей;
— инженерная (прикладная) геодезия изучает методы геодезических работ, выполняемых при изысканиях, проектировании, строительстве и эксплуатации различных зданий и сооружений.
-космическая(спутниковая геодез.)-рассматривает методы координатн.описаний движения искуств. спутников земли в режиме реального времени.
Задачи инженерной геодезии:
1) топографо-геодезические изыскания различных участков, площадок и трасс с целью составления планов и профилей;
2) инженерно-геодезическое проектирование — преобразование рельефа местности для инженерных целей, подготовка геодезических данных для строительных работ;
3)Геодезические разбивочные работы:- вынос проекта в натуру, детальная разбивка осей зданий и сооружений;
4) геодез.выверка конструкций и технологического оборудования при установке их в проектное положение,
5) наблюдения за деформациями зданий и сооружений.
При топографо-геодезических изысканиях выполняют:
а) измерение углов и расстояний на местности с помощью геодезических приборов (теодолитов, нивелиров, лент, рулеток и др.);
б) вычислительную (камеральную) обработку результатов полевых измерений на ЭВМ;
в) графические построения планов, профилей, цифровых моделей местности (ЦММ).
Исторические сведения о развитии геодезии.
Геодезия – возникла в древности. Она возникла и развивалась исходя из практических запросов человека(необходимость ориентирования на местности, межевание земель, определение площади участк,
при строительстве сооружений, определен.форм,выполн. измерен.на местности, по их результатам задавали уклоны водотоков,составл.чертежи участков земн.поверхн. и сооружений на ней.
В дренв.Египте, Греции 4 век до н.э исп. Различные тех.средства:отвесы, угольники, водн.уровни, угломерн.устройств и так стала формироватс геометрия (ЗЕМЛЕИЗМЕРЕНИЕ).В дальнейшем геометрия и геодезия получили свои теоритич. и практич. задачи. Основные теоремы, кот.формировали основы геометрии-Пифагоров треугольник служил для построен. угла на метсности, а число «пи» для расчёта R окружности.
В это ж время создвались простейшие приборы: мерные шнуры, отвесы,угольники,водн.уровни). Голандский учёный Снелиус предложил определять большие расст. методом Триангуляции. К 1795г. во Франции была установлена единица измерения длины – метр(раная 1/40.000000 длины дуги Парижского меридиана.Первые теоретич.работы на тер.РБ проведены были в 1816-1821 корпусом воен.фотограф.В России в Виленск.губерни была созд. Первая сеть триангуляции. В 1969 году на смену оптико механич.-приборам стали внедрять электрон.цифровые измерит.комплексы и компьютерные технологии.
Форма и размеры Земли – геоид, общеземной эллипсоид,земн.шар.
Реальная поверхность земной коры представляет собой рельеф с сочетанием
неровностей различной величины и формы. Фигура земли формируется под действием сил внутреннего тяготения и центробежной силы. Принято считать что земля имеет две поверхности: физическую- образованную твердой оболочкой земли и уровневую поверхность (Мировой океан(70%)) мысленно продолженную под сушей.(геоід)
Геоид – гладкая всюду выпуклая поверхность,образован.уровнем воды мирового океана в состоянии полного покоя и ранвовесия мыслено продолженая под материками и к каждой её точки вектор силы тяжести явл.нормалью к ней. Сущ.различные системы высот. В РБ принята Балтийская система высот за отсчётную поверхность которой принята поверхность геоида,проходящая через нуль Крондштадского футштока. Из-за неравномерного распределения плотности в земной коре и рельефа поверхность геоида имеет
глобальные и локальные волны и не имеет строгого геометри
ческого описания, поэтому невозможно решение на ней задач
вычисления и передачи координат точек земной поверхности.
Для решения этих задач в геодезии используют математиче
скую модель — общий земной эллипсоид, представленный эл
липсоидом вращения, сжатым у полюсов, ось вращения кото
рого и геометрический центр совпадают с осью вращения и
центром масс Земли. Системы геодезич.координат((широт ф, долгот А.), отнесённые к пов-ти эллипсоида назыв. общеземными геоцентрическими.Под руководством Красовского были получены параметры общего земного элипсоида(а=6378245, в=6356263, £=1/298,3 полярное сжатие).
его -(референц-элипсоид) поверхность проецировали центры геодезическ.пунктов полигонов триангуляции 1-ого класса и таким образом на поверхн эл. Была закреплена сис-ма координат СК-42, кот. до настоящего времени исп. на терр. РБ. Сейчас на поверхности эллипсоида была закреплена сис-ма геодезич.координат СК-95.К настоящему времени получены современные общеземные геоцентрические сис-мы координат. Примерами таких систем служат WGS-84(США), ПЗ-90 (Россия).
Во многих практических маркшейдерско-геодезических рас
четах общий земной эллипсоид и референц-эллипсоид заме
няются их более простой моделью — земным шаром радиуса
R = 6371 км (объем земного шара равен объему земного эл
липсоида). Длина экватора L на эллипсоиде Ф.Н. Красовского
равна 2па, или 40 075 км, на земном шаре 2kR, или 40 000 км).
4. Метод проекции в геодезии: ортогональная проекция объектов земной поверхности на сферу, на плоскость, размеры площадок, которые можно считать плоскими прив в плане, учет кривизны Земли при определении превышений.}
Метод ортогональной проекции на горизонтальную плоскость. Иначе методо горизонтальной проекции, применяется при выполнении геодезических работ для отображения их данных на горизонтальной плоскости в виде числовых величин и картографических чертежей.
чки контура АВСМ земной поверхности (рис. 1.3, а) проецируют на уровенную поверхность Ру отвесными линиями. На уровенной поверхности точки а’, Ь’, с’, m’; линии m’а’, m’с; а’Ь’, …, а также контур db’c’m` представляют отвесные проекции соответствующих элементов контура АВСМ. Для ограниченной территории на горизонтальной плоскости Рт оргого-
нальная проекция осуществляется практически параллельными вертикальными лучами: получаются точки а, Ь, с, m; линии mа, mс, аЬ, а также контур abcm. В инженерной практике гори
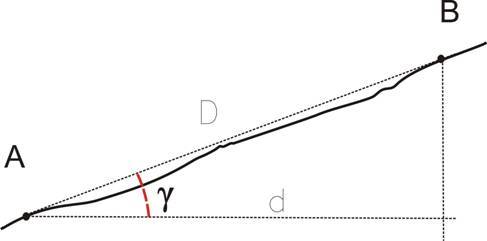
зонтальную плоскость Рт приближают к уровенной поверхности на территории города, промышленного предприятия. Отрезок прямой линии МА длиной D (см. рис. 1.3, а) принадлежит вертикальной плоскости m’МАа’. Угол наклона прямого отрезка МА измеряется относительно горизонтальной плоскости или параллельной ей прямой линии МА’ (рис. 1.3, б). Длина d проекции та отрезка МА на горизонтальную плоскость называется горизонтальным проложением наклонной прямой линии и вычисляется по формуле d= D cosv(ню). (1.4)
Горизонтальные углы. В соответствии с методом ортогональной проекции на горизонтальную плоскость (горизонтальной проекции) в геодезии измеряют горизонтальный угол между направлениями МА и МС (см. рис. 1.3, а), который определяется как двугранный угол р между вертикальными плоскостями АМт’а’ и СМт’с’, проходящими через общую отвесную
линию Мт’ и заданные точки местности А и С. Поскольку горизонтальная плоскость РТ и уровенная поверхность Ру в точках m u m ‘ перпендикулярны отвесной линии Mmm’, то гори
зонтальный угол β будет одинаков на малых площадках уровенной поверхности и горизонтальной плоскости.Площади. Исходя из формулы (1.4), можно рассчитать, на ка
кую величину преуменьшена площадь наклонного участка земной поверхности в проекции на горизонтальную поверхность.
Учет кривизны земной поверхности в инженерно-геодезических работах. Фактор кривизны Земли учитывается при картографировании ее поверхности и в ряде инженерно геодезических задач, например при измерении высот точек и расчете размеров участков на сфере, которые на практике можно принимать плоскими. При рассмотрении фактора кривизны используем шаровую модель Земли.
Учет кривизны Земли при измерении высот. Пусть точки Tо и Со — вертикальные проекции точек T и С поверхности Земли на сферу по радиусам R = ТО и R = СО рис. 1.2, а).
В точке To проведем горизонтальную линию ToC1 — касательную к сфере. Точка C1 представляет вертикальную проекцию точки С на касательную ToС1, а вертикальное расстояние CoC1 = Δh выражает влияние фактора кривизны на измерения высот точек, определяемых относительно горизонтальных линий:
или
Для различных расстояний d при R = 6371 км по формуле (1.1) вычислим значения ДА и получим следующие результаты
(табл. 1.1).
Величина учитывается как поправка при расчете высоты точки С1 относительно поверхности G сферы или практически относительно основной уровенной поверхности Go- Несовпадение между уровенной поверхностью Go и горизонтальной плоскостью T0C1 необходимо учитывать при строительстве ряда сооружений, например тоннелей (рис. 1.2, б). Если тоннель проектировать в вертикальном разрезе прямолинейным по оси М1Т1, то после его строительства подземные и дождевые воды будут стекать относительно уровенной поверхности GG1 (и отвесных линий) к средней его зоне N .
я обеспечения естественного стока тоннели строят с подъемом их средней части, например по профилю МВТ. Учет фактора кривизны Земли при измерении расстояний. Согласно рис. 1.2, а расстояния d и s между проекциями точек T и С на плоскость (точки T0 и С1) и на сферу (точки T0 и С1) различаются за счет фактора кривизны Земли на абсолютную величину
где угол = s /R и выражен в радианах. Значение d вычисляется и по приближенной формуле
(1.2)
Относительная величина Ad I d разности длин d и s получается из формулы (1.2):
(1.3)
Из формулы (1.3) рассчитываются на сферической поверхности размеры участка, в пределах которого можно не учитывать влияние фактора кривизны при условии, что допускается относительная величина искажения длины d / d — = 1 /1 ООО ООО (1 мм / 1 км). Решив уравнение (1.3), получаем d — 11 км — радиус участка, который отвечает поставленному
условию. Если принять иную величину допуска, например
d / d = 1 / 200 ООО (5 мм /1 км), то плоским можн считать участок на сферической и уровенной поверхности радиусом 25 км.
5. Системы координат, применяемые в геодезии(глобальные, зональные в проекции Гаусса-Крюгера, местные).
Глобальные координаты
Для решения геодезических задач в глобальном масштабе используются различные системы глобальных(общеземных) координат: Географические, геодезические, астрономические, пространственные, прямоугольные.
Географические координаты используются когда нет необходимости учитывать сжатие земного элипсойда, что допустима для создания карт мелких масштабов. Положение точек земной поверхности в проекции на поверхность земного шара определ. угловыми величинами относительно исходных плоскостей.
Плоскости экватора и плоскости гринвичского меридиана.
Плоскость экватора проходит через центр элипсойда перпендикулярна его оси вращения PP1 . Экватор представляет окружность – линию пересечения поверхности земного шара с плоскостью экватора.
Географическая параллель см. MN явл. окружн.,кот. образуется при пересечении земного шара плоскостью параллельно плоскости экватора.
Географическая широта
угол между нормалью к поверхности земного шара и плоскости экватора. Широты отсчитываются от экватора к северному полюсу – со знаком + и к югу со знаком — . широта экватора равна 0, а севера + 90о
Географическая долгота — двухгранный угол между плоскостью географического меридиана в точке N и плоскостью Гринвичского меридиана для отсчета долгот. Долготы отсчитываются на восток от 0о до 360о или же на восток от 0 до 180о с указанием « восточная долгота» или на запад от 0 до – 180о с указанием «западная долгота».
Астрономические определяю путём наблюдения звезд при помощи астрономических приборов с использованием радиосигналов точного времени.
Геодезические координаты близки географически но отличия в то что они отсчитываются по нормалям к поверхности референц-эллипсоида.
Системы геоцентрических пространственных прямоугольных координат применяются в спутниковых системах позиционирования. Это вызвано тем,что координато несущие точки являются созвездиями специальныз искусственных спутников Земли, которые обращаются по орбитам вокруг центра масс Земли на высотах приблизительно 20т. Км. Всемирная геоцентрическая система координат WGS – 84 (США) поддерживается созвездием GPS-NAVSTAR рекомендовано к практическому применению международным союзом геодезии и геофизики.
Пространственные прямоугольные координаты в точке N определены отностильно центра масс земли m и координатных осей X,Y,Z (см.рис 1.4)
Геоцентрическая система ПЗ-90 (параметры земли) РФ, поддерживается созвездием ГЛОНАСС является аналогом системы WGS-84(см.рис 1.4)
Источник: megaobuchalka.ru
Предмет и задачи геодезии, ее связь с другими науками
Геодезия – это наука, рассматривающая методы и способы измерения земной поверхности, применение которых дает возможность определять форму и размеры земли, а также производить съемку (измерения) отдельных ее частей для изображения на картах, планах используемых для создания различных инженерных сооружений.
Геодезия включает в себя высшую и космическую геодезии, топографию, фотограмметрию и инженерную геодезию.
– Высшая геодезия – изучает фигуру и размер земли, методы определения координат точек на поверхности для территории всей страны.
– Космическаягеодезия – решает геодезические задачи с помощью искусственных спутников земли.
– Топография – рассматривает способы изучения земной поверхности, и изображение ее на картах и планах.
– Фотограмметрия – решает задачи измерений по аэро- фото- и космическим снимкам для различных целей.
– Инженерная геодезия – изучает методы геодезического обеспечения при разработке проектов, строительств, эксплуатации различных сооружений, а также при изучении освоении и охране природных ресурсов.
Геодезические работы разделяются на полевые и камеральные.
– Полевые работы состоят из измерений горизонтальных и вертикальных углов, а также горизонтальных, наклонных и вертикальных расстояний.
– Камеральные работы состоят из вычислений результатов полевых измерений и графических построений.
Формы и размеры земли
Физическая поверхность земли представляет собой сочетание возвышенностей и углублений, которые, как правило, заполнены водой, поскольку большую часть поверхности земли составляет поверхность океанов и морей, то за общую фигуру земли приняли очертание поверхности воды в спокойном ее состоянии мысленно продолженным под материками. В любой точке эта поверхность перпендикулярна и т.о. везде горизонтальна, такая поверхность называется уровенной, приуроченная к среднему уровню океана и называется среднеуровенной поверхностью.
Тело ограниченное среднеуровенной поверхностью называется геоидом. Вследствие неравномерности распределения масс в земной коре, поверхность геоида не является правильной геометрической поверхностью, поэтому, для изучения фигуры земли, используют правильное тело эллипсоид вращения, фигура, которая близка к геоиду. Она характеризуется большой и малой полуосями, и полярным сжатием.
– формула полярного сжатия.
Размеры земного эллипсоида, принятые как обязательные в нашей стране:
а=6 378 245 м
в=6 356 863 м
α=1:298
В исключительных случаях без ущерба для точности можно принимать землю за шар с R=6 371.11 км.
Системы координат
– делятся на плановые и высотные.
· Плановые системы координат. Географические координаты.
За основную поверхность проекции принимают поверхность эллипсоида и геоида.
За основные координатные линии принимают меридианы и параллели.
Меридиан – это сечение эллипсоида плоскостью проходящей через полярную ось NS.
Параллель – сечение эллипсоида плоскостью перпендикулярно7й полярной оси NS.
Долгота– это двугранный угол между плоскостью нулевого меридиана и плоскостью меридиана проходящего через определяемую точку. Отсчитывается к западу и востоку от нулевого меридиана, изменяется от 0º до 180º.
Широта – угол между плоскостью экватора и нормалью к эллипсоиду (отвесной линией) отсчитывается к северу и югу от экватора и изменяется от 0º до 90º.
· Плоские прямоугольные координаты
– представляют собой две взаимно перпендикулярные прямые лежащие в горизонтальной плоскости. Точка пересечения прямых начало счета координат. Одна из прямых совпадает с меридианом и принимается за ось х, с положительным направлением на север, а вторая за ось у с положительным направление на восток.
Эта система координат применяется на небольших участках земной поверхности размерами не более 20х20 км.
В некоторых случаях ось х не совпадает с меридианом, в этом случае системакоординат называется частной или условной. Частные системы применяются при производстве инженерно–технических работ.
· Система координат Гаусса–Крюгера (зональная система координат)
В геодезии на плоскости изображаются значительные участки земной поверхности. Для этого применяются различные проекции, дающие возможность переносить изображение на плоскость при помощи математических законов. Для геодезии выгодно чтобы изображение не имело искажения в углах между направлениями (равноугольные проекции или конформные). К этой проекции изображение контуров будет подобным, масштаб практически постоянным и не зависеть от направления, искажения будут возникать только в длинах линий.
Суть проекции и соответствующей системы координат заключается в следующем.
1. Земной эллипсоид при помощи меридианов делится на 6º или 3º зоны. Зоны нумеруют к востоку от нулевого меридиана, средний меридиан каждой зоны называется осевым.
2. Каждая зона в отдельности проектируется на плоскость таким образом, чтобы осевой меридиан и экватор изобразились прямыми линиями без искажений. Осевой меридиан принимается за ось х, с положительным направление на север, а экватор с положительным направлением на восток. Линии параллельны осевому меридиану и экватору, и образуют координатную сетку.
Искажения в этой системе координат возрастают по мере удаления от осевого меридиана (искажается длина). На границе зоны искажения длин линий будет ≈1/1500 для 6º зоны и ≈1/6000 для 3º зоны. Поправка за искажения длины линий будет вычислять по формуле .
D – длина отрезка
R – радиус земли
Y – средняя ордината отрезка.
3. Поскольку внутри каждой зоны системы координат одинаково возникают определенные положения точки на земной поверхности. Для установления зоны, в которой расположена точка, к значению ординаты слева приписывают номер зоны:
уа=1 532 371.15
ув=2 532 371.15
Чтобы не иметь отрицательных ординат точкам осевого меридиана условно приписывается ордината 500км.
Высоты точек в геодезии называются отметками.
Отметка – это отвесное расстояние от начала счета высот до точки.
Если за начало счета высот принимать среднюю уровенную поверхность, система высот называется абсолютной, а отметки абсолютными.
В нашей стране за начало счета прият нуль Кранштадтского футштока, и система высот называется Балтийской.
Если за начало счета высот принимается произвольная уровенная поверхность, то система высот называется относительной, отметки относительными.
В горном деле за начало счета высот принимают отметку устья вскрываемой выработки.
Источник: helpiks.org
2.1. Форма и размеры Земли
Изучение формы и размеров Земли включает решение двух задач. Это — установление некоторой сглаженной, обобщенной, теоретической фигуры Земли и определение отклонений от нее фактической физической поверхности.
Учитывая, что поверхность океанов и морей составляет 71% поверхности Земли, а поверхность суши — только 29%, за теоретическую фигуру Земли принято тело, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками, и называемое геоидом.
Поверхность, в каждой своей точке перпендикулярная к отвесной линии (направлению силы тяжести), называется уровенной поверхностью. Из множества уpовенных поверхностей одна совпадает с поверхностью геоида.
Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически, что необходимо для решения геодезических задач. При решении геодезических задач геоид заменяют близкими к нему геометрически правильными поверхностями.
Так, для приближенных вычислений Землю принимают за шар с радиусом 6371 км.
Ближе к форме геоида подходит эллипсоид – фигура, получаемая вращением эллипса (рис. 2.1) вокруг его малой оси. Размеры земного эллипсоида характеризуют следующими основными параметрами: a — большая полуось, b — малая полуось, a — полярное сжатие и e – первый эксцентриситет меридианного эллипса, где и .
|
|
Рис. 2.1. Меридианный эллипс: Рс – северный полюс; Рю – южный полюс
|
Различают общеземной эллипсоид и референц-эллипсоид.
Центр общеземного эллипсоида помещают в центре масс Земли, ось вращения совмещают со средней осью вращения Земли, а размеры принимают такие, чтобы обеспечить наибольшую близость поверхности эллипсоида к поверхности геоида. Общеземной эллипсоид используют при решении глобальных геодезических задач, и в частности, при обработке спутниковых измерений. В настоящее время широко пользуются двумя общеземными эллипсоидами: ПЗ-90 (Параметры Земли 1990 г, Россия) и WGS-84 (Мировая геодезическая система 1984 г, США).
Референц-эллипсоид – эллипсоид, принятый для геодезических работ в конкретной стране. С референц-эллипсоидом связана принятая в стране система координат. Параметры референц-эллипсоида подбираются под условием наилучшей аппроксимации данной части поверхности Земли. При этом совмещения центров эллипсоида и Земли не добиваются.
В России с 1946 г. в качестве референц-эллипсоида используется эллипсоид Красовского с параметрами: а = 6 378 245 м, a = 1/ 298,3.
2.2. Системы координат, применяемые в геодезии
Для определения положения точек в геодезии применяют пространственные прямоугольные, геодезические и плоские прямоугольные координаты.
Пространственные прямоугольные координаты. Начало системы координат расположено в центре O земного эллипсоида (рис. 2.2).
|
|
Рис. 2.2. Земной эллипсоид и координаты: Х, Y , Z – пространственные прямоугольные; B, L, H — геодезические; G — Гринвич
|
Ось Z направлена по оси вращения эллипсоида к северу. Ось Х лежит в пересечении плоскости экватора с начальным — гринвичским меридианом. Ось Y направлена перпендикулярно осям Z и X на восток.
Геодезические координаты. Геодезическими координатами точки являются ее широта, долгота и высота (рис. 2.2).
Геодезической широтой точки М называется угол В, образованный нормалью к поверхности эллипсоида, проходящей через данную точку, и плоскостью экватора.
Широта отсчитывается от экватора к северу и югу от 0° до 90° и называется северной или южной. Северную широту считают положительной, а южную — отрицательной.
Плоскости сечения эллипсоида, проходящие через ось OZ, называются геодезическими меридианами.
Геодезической долготой точки М называется двугранный угол L, образованный плоскостями начального (гринвичского) геодезического меридиана и геодезического меридиана данной точки.
Долготы отсчитывают от начального меридиана в пределах от 0° до 360° на восток, или от 0° до 180° на восток (положительные) и от 0° до 180° на запад (отрицательные).
Геодезической высотой точки М является ее высота Н над поверхностью земного эллипсоида.
Геодезические координаты с пространственными прямоугольными координатами связаны формулами
X = (N + H) cosB cosL,
Y = (N+H) cosB sinL,
Z = [(1 — e2) N+H] sinB,
где e — первый эксцентриситет меридианного эллипса и N — радиус кривизны первого вертикала. При этом N=a/(1 — e2 sin2B)1/2.
Геодезические и пространственные прямоугольные координаты точек определяют с помощью спутниковых измерений, а также путем их привязки геодезическими измерениями к точкам с известными координатами.
Отметим, что наряду с геодезическими существуют еще астрономические широта и долгота. Астрономическая широта j это — угол, составленный отвесной линией в данной точке с плоскостью экватора. Астрономическая долгота l – угол между плоскостями Гринвичского меридиана и проходящего через отвесную линию в данной точке астрономического меридиана. Астрономические координаты определяют на местности из астрономических наблюдений.
Астрономические координаты отличаются от геодезических потому, что направления отвесных линий не совпадают с направлениями нормалей к поверхности эллипсоида. Угол между направлением нормали к поверхности эллипсоида и отвесной линией в данной точке земной поверхности называется уклонением отвесной линии.
Обобщением геодезических и астрономических координат является термин – географические координаты.
Плоские прямоугольные координаты. Для решения задач инженерной геодезии от пространственных и геодезических координат переходят к более простым – плоским координатам, позволяющим изображать местность на плоскости и определять положение точек двумя координатами х и у.
Поскольку выпуклую поверхность Земли изобразить на плоскости без искажений нельзя, введение плоских координат возможно только на ограниченных участках, где искажения так малы, что ими можно пренебречь. В России принята система прямоугольных координат, основой которой является равноугольная поперечно–цилиндрическая проекция Гаусса. Поверхность эллипсоида изображается на плоскости по частям, называемым зонами. Зоны представляют собой сферические двуугольники, ограниченные меридианами, и простирающиеся от северного полюса до южного (рис. 2.3). Размер зоны по долготе равен 6°. Центральный меридиан каждой зоны называется осевым. Нумерация зон идет от Гринвича к востоку.
|
|
Рис. 2.3. Деление поверхности Земли на координатные зоны: G – Гринвич |
Долгота осевого меридиана зоны с номером N равна:
l0 = 6°× N — 3° .
Осевой меридиан зоны и экватор изображаются на плоскости прямыми линиями (рис. 2.4). Осевой меридиан принимают за ось абсцисс x, а экватор — за ось ординат y. Их пересечение (точка O) служит началом координат данной зоны.
|
|
Рис. 2.4. Изображение координатной зоны на плоскости: О – начало координат (х0=0; у0=500 км). |
Чтобы избежать отрицательных значений ординат, координаты пересечения принимают равными x0 = 0, y0 = 500 км, что равносильно смещению оси х к западу на 500 км.
Чтобы по прямоугольным координатам точки можно было судить, в какой зоне она расположена, к ординате y слева приписывают номер координатной зоны.
Пусть например, координаты точки А имеют вид:
xА = 6 276 427 м
yА = 12 428 566 м
Эти координаты указывают на то, что точка А находится на расстоянии 6276427 м от экватора, в западной части (y < 500 км) 12-ой координатной зоны, на расстоянии 500000 — 428566 = 71434 м от осевого меридиана.
Для пространственных прямоугольных, геодезических и плоских прямоугольных координат в России принята единая система координат СК-95, закрепленная на местности пунктами государственной геодезической сети и построенная по спутниковым и наземным измерениям по состоянию на эпоху 1995 г.
Местные системы прямоугольных координат. При строительстве различных объектов часто используют местные (условные) системы координат, в которых направления осей и начало координат назначают, исходя из удобства их использования в ходе строительства и последующей эксплуатации объекта.
Так, при съемке железнодорожной станции ось у направляют по оси главного железнодорожного пути в направлении возрастания пикетажа, а ось х – по оси здания пассажирского вокзала.
При строительстве мостовых переходов ось х обычно совмещают с осью моста, а ось y идет в перпендикулярном направлении.
При строительстве крупных промышленных и гражданских объектов оси x и y направляют параллельно осям строящихся зданий.
2.3. Системы высот
Счет высот в инженерной геодезии ведут от одной из уровенных поверхностей.
Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот.
Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. На рис. 2.5 отрезки отвесных линий Аа и Вв — абсолютные высоты точек А и В.
Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. На рис. 2.5 отрезки отвесных линий Аа¢ и Вв¢ — условные высоты точек А и В.
В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока.
Численное значение высоты принято называть отметкой. Например, если высота точки А равна HА = 15,378 м, то говорят, что отметка точки равна 15,378 м.
|
|
Рис. 2.5. Абсолютные и условные высоты: a¢b¢ – уровенная поверхность; ab –поверхность геоида; Ab² – уровенная поверхность точки A;
|
Разность высот двух точек называется превышением. Так, превышение точки В над точкой А равно
hAB = HВ — HA.
Зная высоту точки А, для определения высоты точки В на местности измеряют превышение hAB. Высоту точки В вычисляют по формуле
HВ = HA + hAB.
Измерение превышений и последующее вычисление высот точек называется нивелированием.
Абсолютную высоту точки следует отличать от ее геодезической высоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2). Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида.
В заключение отметим, что точное определение положения поверхности геоида в области материков невозможно. Поэтому в России принято отсчитывать высоты от близкой к геоиду, но доступной точному определению вспомогательной поверхности, названной квазигеоидом. Высоты, отсчитываемые от поверхности геоида, называются ортометрическими высотами, а отсчитываемые от поверхности квазигеоида – нормальными высотами. На результаты измерений, выполняемых в инженерной геодезии, различия в двух названных системах высот влияния не оказывают, и в дальнейшем мы их различать не будем, а будем пользоваться введенным выше обобщенным понятием – абсолютные высоты.
Источник: injzashita.com
Лекция 1. гЕОДЕЗИЯ: Общие сведения, понятие о формах и размерах Земли
Оглавление
1. Предмет геодезии. 1
2. Форма и размеры Земли. 1
3. Метод проекций в геодезии. 3
4. Электронные и цифровые карты. 4
1. Предмет геодезии
Слово «геодезия»: Ge (гео) – земля и Daio (дайдзо) – делю, разделяю.
Сегодня геодезия – система наук об определении формы и размеров Земли и об измерениях на земной поверхности для отображения её на планах и картах.
В процессе своего развития геодезия разделилась на ряд самостоятельных научных и научно-технических дисциплин.
1. Геодезическая астрономия
2. Геодезическая гравиметрия
3. Космическая (спутниковая) геодезия
4. Радиогеодезия.
Вышеперечисленные науки относятся к высшей геодезии.
5. Геодезия или топография
6. Гидрография
7. Картография
8. Фототопография
9. Фотограмметрия
10. Маркшейдерия
11. Инженерная или прикладная геодезия.
2. Форма и размеры Земли
Историческая справка об эволюции представлений о форме Земли:
· Впервые к выводу о шарообразности Земли пришел древнегреческий ученый Пифагор (ок. 580–500 до н. э.) в 530 г. до н. э.
· Научно доказал это Аристо–322 до н. э.) в IV в. до н. э.
· Во II в. до н. э. древнегреческий ученый Эратосфен Киренский (ок. 276–l94 до н. э.) впервые сравнительно точно определил средний радиус земного шара.
· На рубеже XVII—XVIII вв. английский ученый И. Ньютон (1643–1727) доказал, что Земля не может иметь форму точного шара, она сплюснута у полюсов.
В различных исследованиях в качестве модели Земли выступают плоскость, шар, эллипсоид вращения, геоид, квазигеоид.
Уровенной поверхностью (УП) называется поверхность, всюду перпендикулярная направлениям силы тяжести.
Свойства УП: 1. Уровенная поверхность — замкнутая поверхность, в каждой своей точке перпендикулярная к отвесной линии, т. е. к направлению силы тяжести. 2. Поскольку потенциал силы тяжести Земли в каждой точке УП имеет одно и то же значение (Потенциал силы тяжести это величина, численно равная работе по переносу единицы массы в поле силы тяжести Земли из бесконечности в данную точку), то уровенных поверхностей можно провести множество.
Нулевая (основная) уровенная поверхность – поверхность, совпадающая со средним значением воды океанов в спокойном состоянии; она образует фигуру, называемую геоидом.
В первом приближении уровенную поверхность Земли можно заменить сферой определенного радиуса (6371,11 км.).
Более близко отражает фигуру Земли эллипсоид, т. е. геометрическая фигура, полученная от вращения эллипса вокруг его малой оси.
Рис. 1.1. Уклонение отвесных линий
Угол между отвесной линией и нормалью к поверхности референц-эллипсоида в данной точке есть отклонение отвеса. Он характеризует наклон уровенной поверхностью земли относительно референц-эллипсоида в этой точке (рис. 1.1).
Эллипсоид, который по своим размерам и положению в теле Земли наиболее правильно представляет фигуру геоида в целом, называют общим земным эллипсоидом.
Эллипсоид, который принят для обработки геодезических измерений, называют референц-эллипсоидом. В разных странах приняты референц-эллипсоиды с разными параметрами.
В российской Федерации в качестве референц-эллипсоида используют эллипсоид Красовского. Параметры этого эллипсоида наиболее точно отражают форму Земли для территории бывшего СССР:
большая полуось – а = 6 м,
малая полуось – в = 6 м
разность полуосей 21,3 км.
Ориентировку референц-эллипсоида в теле Земли осуществляют по исходным геодезическим датам: координатам начального пункта ГГС (пункт Пулково вблизи Санкт-Петербурга), исходному азимуту и высоте поверхности эллипсоида над поверхностью квазигеоида.
3. Метод проекций в геодезии
Метод ортогонального проектирования – реальную физическую поверхность Земли проектируют на плоскость или уровенную поверхность отвесными линиями (линии проектирования перпендикулярны поверхности, на которую проектируют).
А) Пусть на плоскости нужно изобразить значительный участок Земли. Тогда мы проектируем сначала на уровенную поверхность отвесными линиями (рис. 1.2).
Рис. 1.2. Проекция большого участка Земли на уровенную поверхность
Расстояние по отвесной линии от уровенной поверхности Земли (нулевой уровенной поверхности) до точки на физической поверхности Земли называется абсолютной высотой (Н).
Расстояние по отвесной линии от условной уровенной поверхности Земли до точки на физической поверхности Земли называется относительной высотой (Н’).
Численное значение высоты называется отметкой точки. Разность двух отметок называется превышением h.
В России высоты отсчитывают от среднего уровня Балтийского моря, поэтому система высот получила название Балтийской системы высот.
Б) Пусть на плоскости необходимо изобразить небольшой участок местности (рис. 1.3).
Линии ав, вс… называюится горизонтальным проложениями (рис. 1.4), а углы ß1 ß2 … – горизонтальными углами.
ав=АВ соsν,
где ν – угол наклона линии местности.
Рис. 1.3. Проекция небольшого участка Земли на плоскость
Рис. 1.4. Проекция небольшого участка Земли на плоскость
4. Электронные и цифровые карты
Недостатки бумажных карт:
· бумага как материал даёт усадку;
· при тиражировании карт на плоттере возникают искажения;
· точность метрических характеристик объектов зависит от масштаба карты.
В настоящее время вместо бумажных карт всё больше используются электронные (ЭК) или цифровые карты (ЦК), цифровые модели местности (ЦММ).
ЦММ – модель земной поверхности или её элементов (объектов и явлений), их существенных признаков и взаимосвязей, подлежащих отображению на карте, представленная в цифровой форме в определённой системе координат.
ЦК – это цифровая модель местности, записанная на машинном носителе в установленных структурах и кодах, сформированная с учётом законов картографической генерализации в принятых для карт проекции, разграфке, системе координат и высот по точности и содержанию, соответствующая карте определенного масштаба (ГОСТ ).
ЭК – это векторная или растровая карта, сформированная на машинном носителе (например, на оптическом диске) с использованием программных и технических средств в принятой проекции, системе координат и высот, условных знаках, предназначенная для отображения, анализа и моделирования, а также решения информационных и расчётных задач по данным о местности и обстановке.
Источник: pandia.ru