Обхват земли
Меня периодически посещает ощущение что многие простые вещи специально излагаются так, чтобы читатель ничего не понимал и тупо заучивал, либо прочувствовал свою ничтожность перед изощренностью науки. Это всецело относится к известному по школьным учебникам феерическому способу Эратосфена измерения окружности земного шара. Может быть он на самом деле вычислял таким извращенским способом, но зачем этот бред тиражировать со школы?
О том, как можно запудрить мозги в простом вопросе, посмотрим на примере вычисления длины окружности Земли в морских милях, который является частным случаем измерения широты местности и длины пройденного пути по меридиану.
Если современному человеку дать задачу вычислить длину окружности Земли в морских милях, он в подавляющем большинстве случаев заглянет в интернет/справочники и решит примерно так: длину окружности Земли например по парижскому меридиану 40.000 км с помощью калькулятора разделит на современную морскую милю 1,852 км и получит 21.598,3 морских миль, что будет близко к действительности.
Теперь покажу как вычислить длину окружности Земли в уме и абсолютно точно. Для этого надо знать только одно: "Морская миля — единица измерения расстояния, применяемая в

В одном угловом градусе 60 минут, в окружности — 360 градусов, то есть в окружности 360х60=21.600 угловых минут, что в данном случае соответствует длине окружности земного шара в 21.600 морских миль. И это — абсолютно точно, поскольку длина окружности земного шара по меридиану является эталоном, а угловая минута-миля — производная единица. Поскольку Земля — не идеальный сфероид, а слегка кривоватый, то мили на разных меридианах будут немного отличаться друг от друга, но это совершенно неважно для навигации, ибо угловая минута — она и в Африке угловая минута.
Широту местности с точностью до градусов вполне можно измерить даже примитивными приспособлениями вроде транспортира с отвесом, который не сильно отличается от реально применявшегося моряками квадранта и по существу то же самое что и астролябия:



Для более точных измерений углов впоследствии был изобретен секстант (мор. арго — секстан):

Современные люди слабо представляют себе что такое аналоговые вычислительные машины и как ими пользоваться. Для того, чтобы вычислить расстояние между двумя точками в меридиональном направлении, надо всего лишь измерить широты точек, а разность широт выраженная в угловых минутах и будет расстоянием между ними в морских милях. Все просто, удобно и практически применимо.
Если уж так сильно хочется выяснить сколько в морской миле стадий, саженей, аршинов или там египетских локтей, надо аккуратно на коленках промерить ими расстояние между точками с известным расстоянием в морских милях-угловых минутах. Но зачем? Как это практически применимо?
Эратосфен будто бы измерял углы с точностью до угловых секунд и разница широт Александрии составила у него 7° 6,7', то есть 7х60=420+6,7=426,7 морских миль (угловых минут). Кажется, что еще надо? Но ему почему-то требуются дни пути верблюдов и стадии. Возникает ощущение чего-то надуманного — фейка или розыгрыша.
Метод Эратосфена согласно В. А. Бронштейн, Клавдий Птолемей, Гл.12. Работы Птолемея в области географии:
"Как известно, метод Эратосфена заключался в определении дуги меридиана между Александрией и Сиеной в день летнего солнцестояния. В этот день, по рассказам лиц, посещавших Сиену, Солнце в полдень освещало дно самых глубоких колодцев и, значит, проходило через зенит. Следовательно, широта Сиены равнялась углу наклона эклиптики к экватору, который Эратосфен определил в 23°51'20". В тот же день и час в Александрии тень от вертикального столбика гномона закрывала 1/50 часть окружности, центром которой служил кончик гномона. Это значит, что Солнце отстояло в полдень от зенита на 1/50 часть окружности, или на 7° 12'. Приняв расстояние между Александрией и Сиеной равным 5000 стадиев, Эратосфен нашел, что окружность земного шара равна 250 000 стадиев. Вопрос о точной длине стадия, принятого Эратосфеном, долгое время служил предметом дискуссий, поскольку существовали стадии длиной от 148 до 210 м <60>.
льшинство исследователей принимали длину стадия 157,5 м («египетский» стадий). Тогда окружность Земли равна, по Эратосфену, 250 000-0,1575 = 39 375 км, что очень близко к действительному значению 40 008 км. Если же Эратосфен пользовался греческим («олимпийским») стадием длиной 185,2 м, то получалась окружность Земли уже 46 300 км.
По современным измерениям <97> широта Музея в Александрии 31°11,7' широта Асуана (Сиены) 24° 5,0', разница широт 7° 6,7', чему соответствует расстояние между этими городами 788 км. Деля это расстояние на 5000, получим длину стадия, использованного Эратосфеном, 157,6 м. Значит ли это, что он использовал египетский стадий?
Этот вопрос сложнее, чем может показаться. Уже одно то, что Эратосфен привел явно округленное число — 5000 стадиев (а, скажем, не 5150 или 4890) не внушает к нему доверия. А если оценка Эратосфена была завышена хотя бы на 15%, получим, что он использовал египетский стадий в 185 м. Решить этот вопрос пока нельзя." via

Теперь обратим внимание на следующие обстоятельства:
— Асуан (Сиена) и Александрия не находятся на одном меридиане, разница по долготе составляет 3°, то есть около 300 километров.
— Эратосфен не измерил расстояние, а принял исходя из дней пути верблюдов, которые ходили явно не по прямой линии.
— Совершенно неясно каким прибором Эратосфен измерял углы с точностью до секунд
— Непонятно какой стадий использован Эратосфеном для измерения расстояний и т.п.
Но при этом он будто бы получил достаточно точный результат! Или историками сделана подгонка под результат?
Из Википедии: «Эратосфен говорит, что Сиена и Александрия лежат на одном меридиане. И поскольку меридианы в космосе являются большими кругами, такими же большими кругами обязательно будут и меридианы на Земле. И поскольку таков солнечный круг между Сиеной и Александрией, то и путь между ними на Земле с необходимостью идёт по большому кругу.
перь он говорит, что Сиена лежит на круге летнего тропика. И если бы летнее солнцестояние в созвездии Рака происходило ровно в полдень, то солнечные часы в этот момент времени с необходимостью не отбрасывали бы тени, поскольку Солнце находилось бы точно в зените; дела и в самом деле обстоят таким образом в [полосе шириной] в 300 стадиев. А в Александрии в этот же час солнечные часы отбрасывают тень, поскольку этот город лежит к югу от Сиены. Эти города лежат на одном меридиане и на большом круге. На солнечных часах в Александрии проведём дугу, проходящую через конец тени гномона и основание гномона, и этот отрезок дуги произведёт большой круг на чаше, поскольку чаша солнечных часов расположена на большом круге. Далее, вообразим две прямые, опускающиеся под Землю от каждого гномона и встречающиеся в центре Земли. Солнечные часы в Сиене находятся отвесно под Солнцем, и воображаемая прямая проходит от Солнца через вершину гномона солнечных часов, производя одну прямую от Солнца до центра Земли. Вообразим ещё одну прямую, проведённую от конца тени гномона через вершину гномона к Солнцу на чаше в Александрии; и она будет параллельна уже названной прямой, поскольку уже сказано, что прямые от разных частей Солнца к разным частям Земли параллельны (а это он откуда знает?). Прямая, проведённая от центра Земли к гномону в Александрии, образует с этими параллельными равные накрестлежащие углы. Один из них — с вершиной в центре Земли, при встрече прямых, проведённых от солнечных часов к центру Земли, а другой — с вершиной на конце гномона в Александрии, при встрече с прямой, идущей от этого конца к концу его же тени от Солнца, там где эти прямые встречаются наверху.
рвый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии [к своему кругу]. Но найдено, что на чаше она составляет пятидесятую часть своего круга. Поэтому и расстояние от Сиены до Александрии с необходимостью будет составлять пятидесятую часть большого круга Земли. Но оно равно 5 000 стадиев. Поэтому весь круг будет равен 250 000 стадиям. Таков метод Эратосфена».
Позднее полученное Эратосфеном число было увеличено до 252 000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. Но если предположить что речь идёт о греческом (178 метров), то его радиус земли равнялся 7 082 км, если египетским (157,5), то 6 287 км. Современные измерения дают для усреднённого радиуса Земли величину 6 371 км, что делает вышеописанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты." via
Обращаю внимание на то, что в Википедии кроме подгонки результатов также сначала говорится об измерении Эратосфеном длины окружности Земли, а в итоге делается вывод о точности вычисления радиуса Земли. В общем, в огороде бузина, а в Киеве — дядька, хоть они и взаимосвязаны.
Диагноз очень простой: в учебниках по-прежнему будут тиражировать не дающий ничего для понимания сущности и практической применимости метод Эратосфена, но ни словом не будут упоминать связку "морская миля — угловая минута" как пример пропорционального мышления древних, потому что современный тренд заточен под дискретные вычислительные машины, а об аналоговых вычислительных машинах древности приходится рассказывать заново.
См. также:
Первобытная тригонометрия
Как люди догадались о сферической форме Земли?
Главный секрет древнерусского зодчества
Аналоговый расчет купола. Секрет Антонио Гауди
За какими "ведьмами" в действительности охотилась инквизиция
Египет, Франция и история метрологии
Мистика математического маятника
Правильная таблица умножения
первоисточник на сайте
Источник: apxiv.livejournal.com
Земля круглая — это общеизвестно. А что мы еще знаем о ее форме и размерах? Кто из нас на память назовет, сколько километров содержит окружность Земли по экватору? А по меридиану? Кто в курсе, когда и каким образом была впервые измерена длина земной окружности? Между тем, эти факты чрезвычайно интересны.
Впервые окружность Земли была измерена древнегреческим математиком по имени Эратосфен, жившим в городе Сиена. В то время ученые уже знали, что Земля по форме представляет собой шар. Наблюдая за небесным светилом в разное время суток, Эратосфен обратил внимание, что в одно и то же время солнце, будучи наблюдаемым из Сиены, располагается точно в зените, при этом в Александрии в тот же день и час отклоняется на некий угол.
Наблюдения проводились ежегодно в день летнего солнцестояния. Измерив данный угол с помощью астрономических инструментов, ученый установил, что он составляет 1/50 часть полной окружности.
Как известно, полная окружность равняется 360 градусам. Таким образом, достаточно знать хорду угла в 1 градус (т. е. расстояние между точками на поверхности Земли, лежащими на лучах с угловым расстоянием между ними в 1 градус). Затем полученную величину следует умножить на 360.
Взяв за длину хорды расстояние между городами Александрией и Сиеной (5 тысяч египетских стадий) и предполагая, что эти города лежат на одном меридиане, Эратосфен произвел необходимые вычисления и назвал цифру, которой равнялась окружность Земли — 252 тысячи египетских стадий.
Для того времени это измерение было достаточно точным, ведь надежных методов измерения расстояния между городами не существовало, и путь от Сиены до Александрии измерялся скоростью движения каравана верблюдов.
Впоследствии ученые разных стран многократно измеряли и уточняли величину, которую составляет длина окружности Земли. В 17 веке голландский ученый по фамилии Сибелиус придумал способ измерять расстояния с помощью первых теодолитов — специальных геодезических приборов. Данный способ был назван триангуляцией и основан на построении большого количества треугольников с измерением базиса каждого из них.
Способ триангуляции применяется и поныне, вся земная поверхность виртуально поделена и расчерчена на большие треугольники.
Российские ученые тоже внесли свой вклад в эти исследования. В 19 веке окружность Земли измерялась в Пулковской обсерватории, руководил исследованием В. Я. Струве.
До середины 17 века Землю считали шаром правильной формы. Но позже были накоплены некоторые факты, свидетельствующие об уменьшении силы земного притяжения от экватора к полюсу. Ученые ожесточенно дискутировали о причинах этого, самой правдоподобной была признана теория о сжатии Земли с полюсов.
Для проверки этой гипотезы Французской академией были организованы две независимые экспедиции (в 1735 и 1736 годах), которые измеряли длину экваториального и полярного градуса соответственно в Перу и в Лапландии. На экваторе градус, как выяснилось, короче!
Впоследствии другие, более точные измерения подтвердили, что полярная окружность Земли короче экваториальной на 21,4 км.
В настоящее время произведены высокоточные измерения с помощью новейших методов исследований и современных приборов. В нашей стране официально утверждены данные, полученные советскими учеными Изотовым А. А. и Красовским Ф. Н. Согласно этим исследованиям, длина окружности нашей планеты по экватору — 40075,7 километров, по меридиану — 40008,55 км. Экваториальный радиус земного шара (т. н. большая полуось) равняется 6378245 метрам, полярный (малая полуось) — 6356863 метрам.
Площадь земной поверхности — 510 миллионов кв. километров, из которых суше принадлежит только 29 %. Объем земного «шарика» — 1083 миллиарда куб. километров. Масса нашей планеты характеризуется цифрой 6Х10^21 тонн. Из них около 7 % приходится на долю водных ресурсов.
Источник: fb.ru
Окружность Земли по экватору 40000 км, а сколько км будет если мерить через полюса?
Именно благодаря вращению образовалась выпуклость вокруг экватора. Исходя из предпосылки, что Земля имеет форму шара, а окружность равна 360 градусам, находим расстояние (хорду) между двумя точками, расположенными на расстоянии градуса и умножаем на 360. Просто? Длина экватора учеными высчитана по формуле 2πR, несмотря на то, что Земля имеет не шарообразную форму, а вытянута в виде эллипса (шара, сплюснутого у полюсов).
Какая длина экватора Земли?
40 075 километров — такова длина экватора. Экватор делит поверхность земного шара на Северное и Южное полушария и служит началом отсчёта географической широты. Это воображаемая линия, которая проходит по поверхности Земли в плоскости, проходящей через ее центр и перпендикулярной оси вращения планеты. Однако достижение границы между Северным и Южным полушариями все равно не позволило определить, чему равна длина экватора. Измеряя время, в течение которого солнечные лучи достигали дна колодца, ученый смог вычислить радиус земного шара и узнать, какова длина экватора.
В результате внутренних процессов в недрах планеты происходит постепенное разогревание ядра и выделение водорода. Данная теория, кроме всего прочего, дает возможность объяснить и массовое вымирание за короткий промежуток времени многих видов древних животных, так называемое триасовое побоище. Так что со временем длина экватора будет увеличиваться.
Чему равна окружность Земли в километрах — как посчитали эту величину? Какова длина окружности земли по экваториальной линии или по меридиану? Это круговая линия, опоясывающая планету и проходящая через её центр. Экватор перпендикулярен оси земного вращения. Учёный измерил угол и обнаружил, что его величина составляет 1/50 часть от целой окружности, равняемой 360 градусам. Выяснилось, что на экваторе градус имеет меньшую длину. Таким образом выяснили, что окружность Земли полярная меньше окружности по экватору на 21,4 километра.
Какой размер имеет окружность Земли
Кто из нас на память назовет, сколько километров содержит окружность Земли по экватору? Кто в курсе, когда и каким образом была впервые измерена длина земной окружности? Измерив данный угол с помощью астрономических инструментов, ученый установил, что он составляет 1/50 часть полной окружности. Таким образом, достаточно знать хорду угла в 1 градус (т. е. расстояние между точками на поверхности Земли, лежащими на лучах с угловым расстоянием между ними в 1 градус).
Линия экватора перпендикулярна оси вращения нашей планеты и находится на равном расстоянии от обоих полюсов. Это помогло ему вычислить длину радиуса Земли и, соответственно, экватора благодаря формуле длины окружности. К тому же в других статьях Эратосфен вычислил Экватор с помощью угла наклона тень когда Солнце освещало дно колодца!! 1. Линия, проходящая по поверхности Земли (экватор), не может проходить и через центр Земли, как у вас написано.
Эратосфен будто бы измерял углы с точностью до угловых секунд и разница широт Александрии составила у него 7° 6,7′, то есть 7х60=420+6,7=426,7 морских миль (угловых минут). Непонятно какой стадий использован Эратосфеном для измерения расстояний и т.п. Первый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии .

Измерение окружности Земли
Вот простой способ измерения окружности (и диаметр) Земли , который скорее всего был использован древними астрономами. Идеальным выбором была бы Звезда, которая близко расположена к небесной оси Северного полюса (с указанием центра оси вращения Земли). Угловой диаметр Луны и Солнца почти одинаковы: 0,5 градуса. Если один из наших астрономов делал это измерение от места расположения в точке(A) возле Гизы (30 0 С), звезда Мицар должна была появиться около 41 градусов над местным горизонтом.
Общая протяженность этой дуги превысила 2800 км. Она охватывала более 25 градусов, что составляет почти 1/14 часть земной окружности. Теоремы Клеро устанавливают связь между формой Земли, ее вращением и распределением силы тяжести на ее поверхности, тем самым были заложены основы нового направления науки — гравиметрии. Геоид — условная поверхность равного потенциала (поверхность равновесия), совпадающая с поверхностью свободно покоящейся воды в открытом океане. Очевидно, что рельеф литосферы в океанах располагается ниже поверхности геоида, а на материках — выше (говорят: «высота над уровнем моря»).
Еще совсем недавно, в 1862 г., немецкий ученый П. Иоселиани, определяя «глубину толстоты земного шара», получил 4536,8 км, что в 11/2 раза меньше действительной величины. Трудно поверить, но еще в 1876 г. в Петербурге была издана брошюра под названием: «Земля неподвижна, популярная лекция, доказывающая, что земной шар не вращается ни около оси, ни около Солнца. В 1841 г. немецкий астроном Ф. Бессель, используя градусные измерения, вычислил радиус Земли и ее сжатие у полюсов, т. е. получил цифры, характеризующие основные элементы земного эллипсоида. Приходится считать также, что северное и южное полушария, как показал русский ученый А. А. Иванов, не вполне симметричны относительно плоскости экватора.
По своим размерам она превосходит только Меркурий, Марс и Плутон. Когда к Солнцу обращена область вокруг Северного полюса, в Северном полушарии лето, а в Южном — зима. Когда к Солнцу обращена область вокруг Южного полюса — наоборот. Мередиан–половина окружности, соответствует _______градусам и ________», категории «география».

Конечно, в результате подобных изучений Эратосфен вычислил приближенную длину радиуса Земли, а значит и экватора. Для вычисления земного экватора необходимо знать радиус планеты. На экваторе широта равна нулю. Длина экватора – это одна из основных характеристик любой планеты.
Магнитное поле Земли в первом приближении представляет собой диполь, полюсы которого расположены рядом с географическими полюсами планеты.
21,3 километра — настолько экватор дальше от центра Земли, чем ее полюса. Из-за вращения земной шар сплюснут с полюсов на 1/298 диаметра. 35 786 километров — на такой высоте над экватором расположена геостационарная орбита, на которой «висят» спутники связи. Сигнал со скоростью света идет туда-обратно всего четверть секунды.
Из-за наклона земной оси высота Солнца над горизонтом в течение года изменяется. Для Земли радиус сферы Хилла (сфера влияния земной гравитации) равен примерно 1,5 млн км[комм. 5]. Это максимальное расстояние, на котором влияние гравитации Земли больше, чем влияние гравитации других планет и Солнца.
Для измерения зенитного расстояния Солнца Эратосфен использовал в качестве угломерного прибора солнечные часы — скафис. Солнца составляет 47 градусов 42 минуты.
Иными словами, метр был определен как 1/10, 000000 расстояния от экватора Земли до Северного полюса измеряется по поверхности окружности (эллипсоида) Земли через долготу Парижа.

Источник: estortenok.ru
Источник:  apxiv
apxiv
Меня периодически посещает ощущение что многие простые вещи специально излагаются так, чтобы читатель ничего не понимал и тупо заучивал, либо прочувствовал свою ничтожность перед изощренностью науки. Это всецело относится к известному по школьным учебникам феерическому способу Эратосфена измерения окружности земного шара. Может быть он на самом деле вычислял таким извращенским способом, но зачем этот бред тиражировать со школы?
О том, как можно запудрить мозги в простом вопросе, посмотрим на примере вычисления длины окружности Земли в морских милях, который является частным случаем измерения широты местности и длины пройденного пути по меридиану.

Если современному человеку дать задачу вычислить длину окружности Земли в морских милях, он в подавляющем большинстве случаев заглянет в интернет/справочники и решит примерно так: длину окружности Земли например по парижскому меридиану 40.000 км с помощью калькулятора разделит на современную морскую милю 1,852 км и получит 21.598,3 морских миль, что будет близко к действительности.
Теперь покажу как вычислить длину окружности Земли в уме и абсолютно точно. Для этого надо знать только одно: «Морская миля — единица измерения расстояния, применяемая в мореплавании и авиации. Первоначально морская миля определялась как длина дуги большого круга на поверхности земного шара размером в одну угловую минуту.»

В одном угловом градусе 60 минут, в окружности — 360 градусов, то есть в окружности 360х60=21.600 угловых минут, что в данном случае соответствует длине окружности земного шара в 21.600 морских миль. И это — абсолютно точно, поскольку длина окружности земного шара по меридиану является эталоном, а угловая минута-миля — производная единица. Поскольку Земля — не идеальный сфероид, а слегка кривоватый, то мили на разных меридианах будут немного отличаться друг от друга, но это совершенно неважно для навигации, ибо угловая минута — она и в Африке угловая минута.
Широту местности с точностью до градусов вполне можно измерить даже примитивными приспособлениями вроде транспортира с отвесом, который не сильно отличается от реально применявшегося моряками квадранта и по существу то же самое что и астролябия:


Для более точных измерений углов впоследствии был изобретен секстант (мор. арго — секстан):

Современные люди слабо представляют себе что такое аналоговые вычислительные машины и как ими пользоваться. Для того, чтобы вычислить расстояние между двумя точками в меридиональном направлении, надо всего лишь измерить широты точек, а разность широт выраженная в угловых минутах и будет расстоянием между ними в морских милях. Все просто, удобно и практически применимо.
Если уж так сильно хочется выяснить сколько в морской миле стадий, саженей, аршинов или там египетских локтей, надо аккуратно на коленках промерить ими расстояние между точками с известным расстоянием в морских милях-угловых минутах. Но зачем? Как это практически применимо?
Эратосфен будто бы измерял углы с точностью до угловых секунд и разница широт Александрии составила у него 7° 6,7′, то есть 7х60=420+6,7=426,7 морских миль (угловых минут). Кажется, что еще надо? Но ему почему-то требуются дни пути верблюдов и стадии. Возникает ощущение чего-то надуманного — фейка или розыгрыша.
Метод Эратосфена согласно В. А. Бронштейн, Клавдий Птолемей, Гл.12. Работы Птолемея в области географии:
«Как известно, метод Эратосфена заключался в определении дуги меридиана между Александрией и Сиеной в день летнего солнцестояния. В этот день, по рассказам лиц, посещавших Сиену, Солнце в полдень освещало дно самых глубоких колодцев и, значит, проходило через зенит. Следовательно, широта Сиены равнялась углу наклона эклиптики к экватору, который Эратосфен определил в 23°51’20». В тот же день и час в Александрии тень от вертикального столбика гномона закрывала 1/50 часть окружности, центром которой служил кончик гномона. Это значит, что Солнце отстояло в полдень от зенита на 1/50 часть окружности, или на 7° 12′. Приняв расстояние между Александрией и Сиеной равным 5000 стадиев, Эратосфен нашел, что окружность земного шара равна 250 000 стадиев. Вопрос о точной длине стадия, принятого Эратосфеном, долгое время служил предметом дискуссий, поскольку существовали стадии длиной от 148 до 210 м <60>. Большинство исследователей принимали длину стадия 157,5 м («египетский» стадий). Тогда окружность Земли равна, по Эратосфену, 250 000-0,1575 = 39 375 км, что очень близко к действительному значению 40 008 км. Если же Эратосфен пользовался греческим («олимпийским») стадием длиной 185,2 м, то получалась окружность Земли уже 46 300 км.
По современным измерениям <97> широта Музея в Александрии 31°11,7′ широта Асуана (Сиены) 24° 5,0′, разница широт 7° 6,7′, чему соответствует расстояние между этими городами 788 км. Деля это расстояние на 5000, получим длину стадия, использованного Эратосфеном, 157,6 м. Значит ли это, что он использовал египетский стадий?
Этот вопрос сложнее, чем может показаться. Уже одно то, что Эратосфен привел явно округленное число — 5000 стадиев (а, скажем, не 5150 или 4890) не внушает к нему доверия. А если оценка Эратосфена была завышена хотя бы на 15%, получим, что он использовал египетский стадий в 185 м. Решить этот вопрос пока нельзя.»

Теперь обратим внимание на следующие обстоятельства:
— Асуан (Сиена) и Александрия не находятся на одном меридиане, разница по долготе составляет 3°, то есть около 300 километров.
— Эратосфен не измерил расстояние, а принял исходя из дней пути верблюдов, которые ходили явно не по прямой линии.
— Совершенно неясно каким прибором Эратосфен измерял углы с точностью до секунд
— Непонятно какой стадий использован Эратосфеном для измерения расстояний и т.п.
Но при этом он будто бы получил достаточно точный результат! Или историками сделана подгонка под результат?
Из Википедии: «Эратосфен говорит, что Сиена и Александрия лежат на одном меридиане. И поскольку меридианы в космосе являются большими кругами, такими же большими кругами обязательно будут и меридианы на Земле. И поскольку таков солнечный круг между Сиеной и Александрией, то и путь между ними на Земле с необходимостью идёт по большому кругу. Теперь он говорит, что Сиена лежит на круге летнего тропика. И если бы летнее солнцестояние в созвездии Рака происходило ровно в полдень, то солнечные часы в этот момент времени с необходимостью не отбрасывали бы тени, поскольку Солнце находилось бы точно в зените; дела и в самом деле обстоят таким образом в [полосе шириной] в 300 стадиев. А в Александрии в этот же час солнечные часы отбрасывают тень, поскольку этот город лежит к югу от Сиены. Эти города лежат на одном меридиане и на большом круге. На солнечных часах в Александрии проведём дугу, проходящую через конец тени гномона и основание гномона, и этот отрезок дуги произведёт большой круг на чаше, поскольку чаша солнечных часов расположена на большом круге. Далее, вообразим две прямые, опускающиеся под Землю от каждого гномона и встречающиеся в центре Земли. Солнечные часы в Сиене находятся отвесно под Солнцем, и воображаемая прямая проходит от Солнца через вершину гномона солнечных часов, производя одну прямую от Солнца до центра Земли. Вообразим ещё одну прямую, проведённую от конца тени гномона через вершину гномона к Солнцу на чаше в Александрии; и она будет параллельна уже названной прямой, поскольку уже сказано, что прямые от разных частей Солнца к разным частям Земли параллельны (а это он откуда знает?). Прямая, проведённая от центра Земли к гномону в Александрии, образует с этими параллельными равные накрестлежащие углы. Один из них — с вершиной в центре Земли, при встрече прямых, проведённых от солнечных часов к центру Земли, а другой — с вершиной на конце гномона в Александрии, при встрече с прямой, идущей от этого конца к концу его же тени от Солнца, там где эти прямые встречаются наверху. Первый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии [к своему кругу]. Но найдено, что на чаше она составляет пятидесятую часть своего круга. Поэтому и расстояние от Сиены до Александрии с необходимостью будет составлять пятидесятую часть большого круга Земли. Но оно равно 5 000 стадиев. Поэтому весь круг будет равен 250 000 стадиям. Таков метод Эратосфена».
Позднее полученное Эратосфеном число было увеличено до 252 000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. Но если предположить что речь идёт о греческом (178 метров), то его радиус земли равнялся 7 082 км, если египетским (157,5), то 6 287 км. Современные измерения дают для усреднённого радиуса Земли величину 6 371 км, что делает вышеописанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.» via
Обращаю внимание на то, что в Википедии кроме подгонки результатов также сначала говорится об измерении Эратосфеном длины окружности Земли, а в итоге делается вывод о точности вычисления радиуса Земли. В общем, в огороде бузина, а в Киеве — дядька, хоть они и взаимосвязаны.
Диагноз очень простой: в учебниках по-прежнему будут тиражировать не дающий ничего для понимания сущности и практической применимости метод Эратосфена, но ни словом не будут упоминать связку «морская миля — угловая минута» как пример пропорционального мышления древних, потому что современный тренд заточен под дискретные вычислительные машины, а об аналоговых вычислительных машинах древности приходится рассказывать заново.

Тур Хейердал не просто выдвинул какие-то теории, он самолично провел множество следственных экспериментов по проверке своих утверждений в отличие от клавиатурных бойцов и многих кабинетных ученых. Так что его труды ИМХО должны быть в режиме «обязательны к прочтению».
Глава «Возможные океанские пути в Америку и из Америки до Колумба»:
«При знакомстве с теорией Хейердала, в том виде, какой она имела в 1961 году, становится ясно, что он подходит к вопросу о миграциях с известными оговорками. Хейердал учитывает огромные трудности, с которыми приходилось сталкиваться человеку прошлого.
Такая сдержанность необходима, потому что теперь повсеместно изменился взгляд на миграции через необозримые просторы океанов. Очень долго считалось (особенно в США), что заселение Нового Света происходило только через Берингов пролив и в определенный отрезок времени в далеком прошлом. И совпадения с теми или иными чертами высокоразвитых культур Старого Света всецело объясняли параллельным развитием.
Ныне эта культурно-историческая доктрина Мунро пересмотрена. Все больше склоняются к тому, чтобы признать, что азиатские народы совершили целый ряд далеких плаваний и открытий. Если говорить об Атлантическом океане, то полагают, что его первыми пересекли не норманны. В пору бурного расцвета миграционных теорий очень полезно прочесть анализ Хейердала, в котором кроме дезориентирующей подчас географической карты, учитываются также ветры и течения.
Нижеследующий текст был опубликован в 1964 году в записках XXXV Международного конгресса американистов, состоявшегося в Мексике в 1962 году. Небольшие сокращения произведены для того, чтобы не повторять материал других глав.
Настоящий доклад представляет собой краткий обзор возможных океанских путей, практически доступных человеку в далекие времена при плаваниях в Америку и из Америки. Я отнюдь не утверждаю, что по всем рассматриваемым ниже маршрутам в самом деле плавали предшественники Колумба, хотя очевидно, что на этих путях древнего человека не подстерегали неодолимые препятствия. И цель обзора не в том, чтобы углубиться в проблемы древнего взаимопроникновения культур, – я анализирую лишь чисто практические вопросы, возникающие у тех, кто допускает возможность трансокеанских сообщений между отдельными областями Старого и Нового Света.
Спору нет, океан куда более серьезно препятствовал географическому распространению первобытного человека, чем пустыня, болото, джунгли или тундра. Но в океане, в отличие от других географических препятствий, есть «тропы», которые вполне можно сравнить с реками. Вот почему утверждение, будто у человека было очень мало надежд перенести долгое трансокеанское плавание, выглядит скороспелым. Для определенных областей необходимы существенные поправки.
Современные этнологи, как правило, проходят мимо двух важных обстоятельств. Они не учитывают, во-первых, что расстояние между двумя полярными точками, лежащими в противоположных концах земного шара (наподобие Северного и Южного полюсов), по экватору ничуть не короче расстояния между ними по дуге большой окружности в любом полушарии и, во-вторых, что путевое расстояние, проходимое судном из одной географической точки в другую, практически не равно расстоянию, измеренному по карте, больше того – путь в одну сторону не равен пути в обратную сторону.
Первое обстоятельство можно проиллюстрировать следующим характерным примером. Разбирая интересное открытие (некоторые общие черты в керамике Японии и Эквадора), (II) редакция журнала «Ньюсуик» (19 февраля 1962 года, стр. 49) заявляет, что Экваториальное противотечение «идет прямо к Эквадору», тогда как «Японское течение делает крюк через северную часть Тихого океана». Обычный, широкоупотребительный оборот речи только вводит в заблуждение. Ведь на самом деле Куросио (Японское течение), якобы делающее крюк, – наиболее короткий и прямой из двух названных путей. В этом можно убедиться, если вместо обманчивой меркаторской проекции (она часто применяется для карт мира; в этой проекции поверхность земного шара приводится к поверхности цилиндра, поэтому приполярные области сильно искажены) обратиться к глобусу, который несравненно вернее передает реальную картину.
Похоже, мало кто из этнологов отдает себе отчет в том, что, если плыть от полуострова Малакка до Эквадора через Алеутские острова, получится прямая линия между этими двумя точками (прямее пути не придумаешь). Бессмысленно искать кратчайший путь по линии экватора: ведь он повторяет кривизну земного шара точно так же, как любая другая дуга большой окружности, только этого не видно на плоской карте Тихого океана.
Китай и Перу – тоже полярные. Расстояние по прямой между тихоокеанским побережьем Южного Китая и Перу через экватор ничуть не короче, чем через Северный или Южный полюс. Между этими двумя противолежащими берегами Тихого океана нельзя провести линию прямее или короче той, которая на меркаторской проекции описывает мнимую дугу через крайний север Тихого океана. Соедините на глобусе проволокой побережье Южного Китая с Перу вдоль экватора и смещайте проволоку вверх, закрепив оба конца, она уляжется даже на маршруте, проходящем через Берингово море.
Называть экватор кратчайшим путем между Юго-Восточной Азией и Южной Америкой так же неверно, как утверждать, что кратчайший путь от Северною до Южного полюса проходит по Гринвичскому меридиану.
Следует помнить, что громадный Тихий океан – не гладкая равнина, а правильное полушарие, одинаково покатое во все стороны. Тогда совсем в другом свете выглядят предпосылки для путешествий аборигенных судов в неизведанном океане. Первобытный мореплаватель в какую бы сторону ни шел, видел себя в центре плоского круга, у него не было карты, которая могла бы сбить его с толку.
Второе обстоятельство, решительно требующее большой осторожности при изучении древних океанских плаваний, связано с неверным определением путевого расстояния между фиксированными точками в море. Абсолютное расстояние между двумя точками можно выразить в милях, обычно оно расходится с действительным, которое нужно проплыть. Просто мы ничего не знаем о путевом расстоянии, пройденном древним мореходом, так как нам неизвестно соотношение между скоростью течения в этой области и технически возможной собственной скоростью судна. Чем меньше собственная скорость судна, тем больше несоответствие между измеренным и действительно пройденным путем.
Вот почему путевое расстояние для современного океанского лайнера может быть совсем иным, чем для примитивного судна, хотя бы они шли по одной и той же прямой, над одним и тем же участком неподвижного океанского дна. Насколько велика эта разница, можно показать на примере трансокеанского плавания на аборигенном судне, в котором участвовал автор.
Абсолютное расстояние от Перу до островов Туамоту приблизительно 4000 миль. А на самом деле плот «Кон-Тики», пройдя от Перу до Туамоту, пересек всего около 1000 миль океанской поверхности. Если представить себе первобытное судно, способное идти с той же собственной скоростью и тоже по прямой, но в противоположном направлении, ему, чтобы попасть с Туамоту в Перу, пришлось бы пройти 7000 миль по океанской поверхности. Дело в том, что за время плавания сама поверхность океана сместилась примерно на 3000 миль (около 50 градусов окружности земного шара). Итак, если говорить о путевом расстоянии, острова Туамоту находятся всего лишь в 1000 миль от Перу, тогда как от Туамоту до Перу для того, кто идет через океан со скоростью плота «Кон-Тики», 7000 миль.
Точно так же абсолютное расстояние между Перу и Маркизскими островами составляет примерно 4000 миль. Но средняя скорость течения в этой области приблизительно 40 миль в день, а это означает, что если аборигенное судно идет на запад с собственной скоростью 60 миль в день, оно на самом деле проходит в день 60 плюс 40, то есть 100 миль, и одолевает весь путь за 40 дней. В обратном направлении при той же собственной скорости оно будет делать 60 минус 40 миль, то есть 20 миль в день, и на путь от Маркизских островов до Перу уйдет 200 дней.

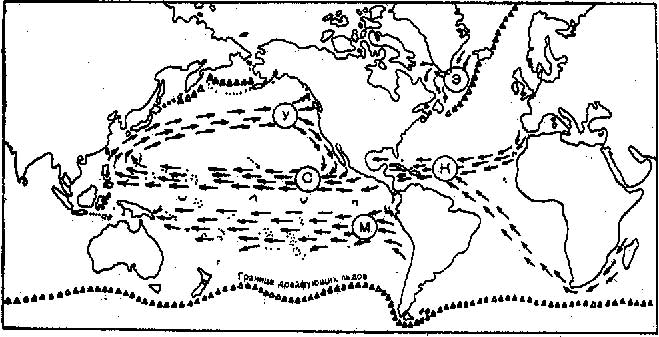
К – маршрут Колумба от Африки до Мексиканского залива; Э – маршрут Лейва Эйрикссона из Северо-Западной Европы до северо-восточной части Северной Америки; У – маршрут Урданеты из Индонезии в Северо-Западную Америку и Мексику; С – маршрут Сааведры из Мексики в Микронезию и Индонезию; М – маршрут Менданьц от Андского побережья в Полинезию и Папуа-Меланезию.
Пусть собственная скорость судна только 40 миль в день, оно все равно будет идти на запад со скоростью 40 плюс 40, или 80 миль, и уже через 50 дней достигнет Маркизских островов. А в обратную сторону при скорости 40 минус 40, то есть ноль миль в день, оно вообще не оторвется от архипелага.
Эти примеры приложимы не только к району, о котором мы говорили, они в той или иной мере распространяются на любые трансокеанские плавания первобытных судов. Наряду с кривизной поверхности великих океанов такой расчет путевого расстояния играет решающую роль, в последующих рассуждениях автора. Расчеты и кривизны, и путевого расстояния составляют ныне основу современной морской навигации, да и прежде, когда еще не было карт, с этими факторами считались все, кто прокладывал путь в Америку и из Америки. И наверно, они были не менее важны для тех, кто выходил в неизведанный океан, когда еще не было никаких описаний, если мы, конечно, допустим мысль, что доисторический человек отваживался пересекать огромную водную пустыню, это вечно движущееся полушарие.
Существует три основных океанских маршрута в Новый Свет (два через Атлантический океан и один через Тихий) и два основных маршрута из Нового Света (оба через Тихий океан). Эти маршруты настолько четко определены, что им можно присвоить названия в честь их исторически известных открывателей.»
Далее кратко рассматриваются показанные в схеме маршруты Лейва Эйрикссона, Колумба, Альваро Менданьи, Альваро Сааведра и Андреса де Урданеты.
В главе «Культурные растения — доказательство доколумбовых контактов с Америкой» рассматриваются: кокосовый орех, бутылочная тыква, банан, хлопчатник (в том числе тетраплоидный 26-хромосомный), ананас, перувианская вишня (Physalis peruviana) и Argemone, ямсовые бобы, собственно ямс (Dioscorea sp.), гибискус (Hibiscus tiliaceus), фасоль обыкновенная(Phaseolus vulgaris), фасоль лимская (Phaseolus lunatus), родственное фасоли растение Canavalia sp.
Некоторые цитаты из главы «Бальсовый плот и роль гуар в аборигенном мореходстве Южной Америки»:
«Грубая зарисовка бальсового плота под парусами была сделана голландским адмиралом Шпильбергеном(16) во время его кругосветного плавания в 1614-1617 годах. Шпильберген сообщает, что на этом плоту команда из пяти аборигенов выходила на два месяца ловить рыбу. Улова, доставленного в Паиту, что лежит в 120 милях южнее перуанского порта Тумбеса, хватило, чтобы снабдить провиантом все голландские корабли, стоявшие в бухте. Рисунок Шпильбергена интересен тем, что команда показана в работе. Два индейца заняты парусом, остальные трое маневрируют гуарами – широкими досками, просунутыми в щели между бревнами; не видно ни весел, ни какого-либо руля. Такие выдвижные шверты были освоены европейскими судостроителями только в 1870 году, то есть через двести пятьдесят лет.
В тексте Шпильберген ничего не говорит о гуарах, он лишь заключает, что плот оказался превосходным судном.
Прошло сто тридцать лет, прежде чем навигационные приемы индейцев настолько заинтересовали двух испанских морских офицеров, Хуана и Ульоа, что они решили проникнуть в тайну аборигенных гуар. Они опубликовали превосходный рисунок бальсового плота в море, передав такие детали, как устройство двуногой мачты с парусами и такелажем, расположение рубки в средней части судна, «камбуза» с открытым очагом и запасом воды в кувшинах на корме, размещение выдвижных швертов в носовой и кормовой частях. Хуан и Ульоа решительно утверждали, что индейская команда, хорошо усвоившая искусство маневрирования выдвижными швертами, при любом ветре могла вести бальсовый плот, как обычный корабль.
Они писали: «До сих пор мы говорили только о конструкции и применении плотов, но главная особенность этих судов заключается в том, что они ходят, лавируют и приводятся к ветру ничуть не хуже килевых судов и почти не подвержены сносу. Достигается это с помощью не руля, а другого приспособления, а именно досок длиной три-четыре метра и шириной около полуметра, которые устанавливают вертикально между бревнами основания как на носу, так и на корме.
Погружая глубоко в воду одни доски и поднимая другие, они ходят в бакштаг, приводятся к ветру, меняют галс, ложатся в дрейф – короче, выполняют все маневры, доступные обычным судам.Изобретение, до сих пор неизвестное самым просвещенным нациям Европы… Если погрузить в воду гуару на носу, судно приводится к ветру, если ее поднять, оно пойдет в бакштаг или спустится под ветер. И если погрузить в воду гуару на корме, плот пойдет в бакштаг, а если поднять, он приводится и идет круче к ветру.
Таков способ, с помощью которого индейцы управляют бальсовыми плотами; порой они ставят пять или шесть гуар, чтобы воспрепятствовать сносу, и ясно, что чем глубже в воду погружены гуары, тем больше сопротивление судна с этой стороны, так как гуары выполняют функцию выдвижных килей (подобно позднейшим швертам), применяемых на небольших парусных судах. Способ управления гуарами настолько легок и прост, что, когда плот ложится на нужный курс, дальше пользуются лишь одной из них, погружая или поднимая ее по мере надобности»(17).
Эти древнеперуанские приемы управления судном произвели такое сильное впечатление на обоих авторов, что они настоятельно предлагали перенять их в Европе.»
… «Затем рассказы о перуанской технике мореходства опубликовали знаменитый ученый и путешественник Александр фон Гумбольдт (1810 год) и его английский коллега Стивенсон (1825 год).(20) Стивенсон оставил превосходное описание бальсовых плотов, которые все еще использовали вдоль побережья бывшего государства Чиму вплоть до Хуанчако, южнее Чикамы. На самых больших плотах стояли бамбуковые хижины с четырьмя-пятью помещениями; такие плоты ходили против ветра и течения на сотни миль с грузом 25-30 тонн, не считая команду и ее провиант.»
… «Французский исследователь мореходства Пари отправился в северо-западную часть Южной Америки, чтобы изучить там бальсовый плот. Он описал этот плот в своем капитальном труде о неевропейских судах, вышедшем в 1841-1843 годах. Сто с небольшим лет назад Пари писал: «В Перу по-прежнему применяют такие же плоты, какие в древности строили аборигены; они настолько приспособлены к местным условиям, что их предпочитают всем другим судам…».
Источник: evan-gcrm.livejournal.com